This is a new music instrument using rational numbers. The article explains the discoveries in harmony which created this instrument.

Click this to play Debussy's Passepied.

Instructions: Green keys on the right play sounds, and purple keys on the left change the harmony. These green text links will play sound. (Make sure your sound is on. If you're on mobile, you will have to tap once before it'll let you play. On iOS, make sure the Silent Mode switch is off.)

⏺ Record▶Play

The insight is that the green keys are multiples of one frequency, which are all the notes that can be played together. This means you can play all the notes simultaneously (volume warning), or any subset. As a consequence, rolling your elbow over the keyboard or sweeping your mouse will sound consonant. If you hold 3 notes and don't hear the 3rd note, then your keyboard can only handle 2 keys at a time, called "2-key rollover". In that case, use the mouse and keyboard simultaneously. On mobile, horizontal view will make the buttons bigger.

This instrument has a moving frequency: the "fundamental".

Green keys play multiples of the fundamental. For example, if the fundamental is 60 Hz, the green key 10 will play 10×60 Hz = 600 Hz. The green key 1 (on Right Shift) will play 1×(the fundamental), which is the fundamental itself. The black dashes show a piano, which lights up when notes are played.

Purple keys move the fundamental by multiplication. For example, if the fundamental is 60 Hz, the purple key 4/3 will move the fundamental to 4/3×60 Hz = 80 Hz. Fractions on the far left (7/6) sound more exotic than fractions in the middle (1/2). To undo a purple move, the purple key above/below it is its inverse, so they undo each other.

Blue keys also move the fundamental, but only while held down. Releasing a blue key will undo its move.

The blue, green, yellow, and red squares show the prime factors of the fundamental. From top to bottom, these squares correspond to the primes 2, 3, 5, and 7. The horizontal position of a square shows the powers of its prime. For example, if the fundamental moves by 9/5 = 3²/5, then the green 3 square will move right 2, and the yellow 5 square will move left 1.

Don't worry if you don't understand some things, or don't know any music theory. The keyboard is designed to sound good even when you don't know what you're doing. Just press some keys on the right, and occasionally press a key on the left. Further goals are to choose some rhythm and try some chords.

An amusing exercise is to start one of the green text links at the top, then press random blue keys to interfere with the performance. This creates a strange alteration.

How harmony works

This section gives a short explanation of harmony. It's new research, so it will be new to everyone, including musicians.

The consonance of a chord is predicted by these factors:

1. Notes close to each other are dissonant, like 15 16. Especially if there are many notes close to each other, like 14 15 16.
2. Frequency ratios with small numbers are consonant. For example, 8 6 is consonant because 8/6 = 4/3 has small numbers. 4 7 is dissonant because 4/7 has the large number 7.
3. Frequencies in arithmetic sequences and sums are consonant. Skipping terms in a sequence is fine: like 4 7 10 16, which skips 13.

This distills harmony into simple rules. We'll describe why these rules appear.

A sound has a collection of frequencies. If two of these frequencies are close, but not equal, then we perceive a beating sound, called "roughness". Roughness causes dissonance. In the following graph: one frequency is 200 Hz, the second frequency is in the x-axis in Hz, and the y-axis is the roughness between them.

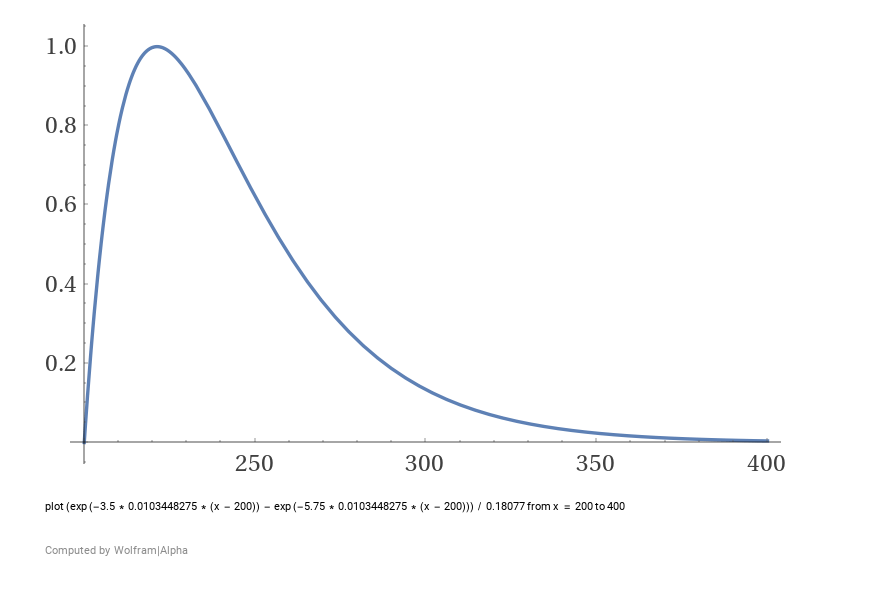
We can see that two frequencies are most dissonant when moderately close. They're consonant when they're either far apart or very very close. This creates the first rule: notes next to each other are dissonant.

A music note usually has a fundamental frequency, like 300 Hz. Playing this note will sound the multiples of 300 Hz: 300 Hz, 600 Hz, 900 Hz, 1200 Hz, etc. Higher multiples (called harmonic overtones) are lower in volume. For consonance, their overtones should be either exactly equal or far apart, which happens when the frequency ratios are small numbers. This creates the second rule.

The new discovery is that roughness appears from the linear combinations (sums and differences) of frequencies. Dissonance is created when these combinations are moderately close to 0, rather than far from 0 or very close to 0. For example, 200 Hz, 310 Hz, 400 Hz is slightly dissonant because 200 - 310 * 2 + 400 = 20, which is close to 0, while 200 Hz, 300 Hz, 400 Hz is consonant. The more terms in the combination, the weaker it is: so 5x + 6y - 3z, with 5 + 6 + 3 = 14 terms, matters a lot less than 2x + y - z, with 4 terms. x - y is the strongest combination, and it gives the original definition for roughness, comparing two frequencies.

(Note: if you're a music researcher, then you've heard of combination tones before, but those are different. Plomp's 1967 paper is the phenomenon here.)

Linear combinations create the third rule. Arithmetic sequences are consonant when exact (12 16 20, 16-12=20-16) and dissonant when inexact (12 15 20). Sums are consonant when exact (6 10 16, 6+10=16) and dissonant when inexact (6 10 15).

The major triad has frequencies 4:5:6 and the minor triad has frequencies 1/4:1/5:1/6. The standard theory of roughness calculates dissonance from pairwise ratios, which are the same for both chords. So it predicts they are equally consonant, which is wrong. Linear combinations explain why the minor chord is more dissonant: the major chord (4 5 6) is an arithmetic sequence and the minor chord (10 12 15) is not.

A more complex example is the dissonant chord 8 10 12 15 18. This is two 4 5 6 chords (major triads) stacked on each other. Existing harmonic theories fail here; they either predict consonance or leave it as a special case. The fix is that the dissonance comes from being an inexact arithmetic sequence. Changing the last two notes, 8 10 12 14 16 is consonant because it is an arithmetic sequence. So linear combinations explain chords that are out of scope for other theories.

If we split the first chord 8 10 12 15 18 into a sequence, it's consonant. And if we split the second chord 8 10 12 14 16, the fourth note has tension. So in sequence form, the second example is more dissonant, which is the reverse of when they were chords! The reason is that linear combinations only apply to overlapping notes (chords), not sequences. For sequences, small numbers in ratios are the source of consonance.

On this instrument, it's easy to calculate the ratios and linear combinations, so harmony is simple. On a piano, harmony is considerably harder, requiring you to count keys, memorize approximations of 2^n/12, and do fractional arithmetic. So musicians generally memorize the harmonies, but you don't need to. It's more fun and satisfying to understand harmony than to memorize harmony. There are too many strange and obscure chords to memorize anyway.

With this explanation of harmony, we can understand the logic behind the instrument. The green keys and their overtones are multiples of a single fundamental frequency N, so their sums and differences are also multiples of N. This means any linear combination is either 0 or at least N away from 0, satisfying the condition for consonance. Thus, the notes harmonize with each other. Conversely, if any key were not a multiple of N, its overtones and linear combinations would be dissonant with the other notes. (There are minor exceptions like 1/2 and 2/3.) So the multiples of a single frequency form a uniquely coherent set, represented by the green keys.

Performing

This instrument has a slight accuracy advantage over a piano, since it uses just intonation instead of 12 equal temperament. 12 equal temperament rounds intervals to enable modulation. This instrument modulates using the purple keys, so it doesn't need rounding. This difference is visualized: when you press green keys, sometimes the cyan square doesn't quite line up with the piano keys below, and the misalignment is the frequency difference. The biggest accuracy improvement is with 7: 5 6 7 is cleaner than the diminished triad, and 4 5 6 7 is cleaner than the dominant 7th. It's more audible at high volume, because roughness scales nonlinearly with volume.

The keys are all close together, so you can play fast and wide intervals without reaching. Fat-fingering multiple keys with one finger is useful rather than dissonant.

The fundamental is analogous to tonality, and purple/blue keys shift the fundamental. The purple keys are ratios, because ratios like 5/4 need fewer presses to modulate than integers like 5. Plus, ratios move pitch less, so random ratios sound good and random integers do not. There's a logical pattern to the green keys that accords with consonance, described at this link.

This pattern in the purple and green keys creates a wonderful map: the physical distance between notes on the keyboard is approximately their dissonance. For example, if you press 1 purple key and move 3 spaces in the green keys, the new note's dissonance is about "4". So you have an easy estimate of consonance, just looking visually at the keyboard. In improv and composition, this helps restrict your attention to the relevant choices. For beginner composers, this guidance is impactful, as they no longer have to test many wrong notes to find the ones which fit.

The numbers on the keyboard allow you to read consonance directly by calculating harmony; you don't have to test chords to know how they'll sound. That's useful when composing, but has no direct benefit for performance.

The disadvantage of this instrument is that you have to press purple/blue keys, which aren't necessary on a piano. These add 25% extra keypresses. The timing can be difficult if a purple key is between two fast notes.

This instrument can't play everything a piano can. It needs 8 thumb keys to be able to, and your computer keyboard doesn't have thumb keys. This comparison isn't quite fair; a piano also can't play everything if simulated by a computer keyboard. But you don't have thumb keys, while you might have a piano, so this is the relevant comparison.

In my testing, this instrument can play all the consonant chords and most of the moderately dissonant chords. It plays chords over 1 fundamental, which encompasses most chords. The remaining chords, like embedded tritones and minor-major chords, require 2 fundamentals and are dissonant. The next section describes this further.

A custom-designed keyboard would enable some cool things. 2 banks of green keys, one for each hand, would let you play any note with either hand. This solves all fingering issues and gives two-handed control of the melody. Purple and blue keys would be moved to the thumbs. Each blue key would modify only one bank of green keys, thus creating a second fundamental, so you can play everything a piano can. Only 48 buttons need complex sensors (polyphonic aftertouch), compared to 76 for a piano. The adjacent keys make 3D expressivity easier to control. The left and right hands can play the timbres of different instruments, so you can be two musicians in one. However, building hardware is out of my reach, so I have no product to sell.

Availability of sheet music is zero. Nobody else uses this instrument, so you have no common platform or shared language with other musicians. If you want to try playing existing songs, there are some rough and tedious steps at this link. In the future, I might write a (midi → Just Intonation) converter to produce some sheet music.

If you know what a DAW is, this webpage can send MIDI messages to it, but you might have to troubleshoot the connection. The DAW and browser must be on the same computer. Chrome will work, Firefox might work, and Safari won't work. On Ubuntu, the default snap browsers won't work, only their deb versions.

The source code is unminified in this page, and at this git repository. If you're simulating a piano on a computer keyboard or on a screen, consider using this layout instead. It can produce 12 equal temperament if needed, because just as 12 equal temperament approximates just intonation, just intonation also approximates 12 equal temperament.

Discussion: Hacker News, Tildes

Author: Kevin Yin

Appendix: Why music matches the instrument's keys

You probably don't want to bother reading this section unless you are really interested in music; it is technical and requires knowing a more complete model of harmony. This model is boringly detailed, but we need it to do calculations. The moral of the story is that the instrument can play almost all tonal music, minus a few dissonant chords. A custom keyboard with thumb buttons can play the remaining chords.

I define a sound as "locally consonant" if it is the most consonant sound in a small region. Instruments without fixed tuning, like voice and violin, gravitate to locally consonant sounds. Mathematically, a sound is locally consonant if perturbing its frequencies makes it more dissonant. An example perturbation is raising 210 Hz to 215 Hz — a small change.

We'll show that the instrument can play most locally consonant sounds. The instrument can play frequencies that are multiples of a single fundamental, and we want to see when locally consonant sounds fit this pattern.

If there are only two frequencies, then they are in an integer ratio by aligning overtones to reduce roughness, so clearing denominators makes them multiples of a fundamental. If there are three or more frequencies, and the frequencies are close enough like 4-5.2-6.2, then lattice tones force them to be in an arithmetic sequence, like 4-5.1-6.2. If two of the numbers are in a small-enough ratio, like 4/6.2 ~ 2/3, then lattice tones, prime-ratio harmony, and overtones will push them to be exactly that small ratio, like 4-5-6.

This process splits sounds into categories:

0. The sounds that the instrument can play: multiples of a single fundamental.
1. The minor triad: 1/4, 1/5, 1/6. Its pairwise ratios are small, so their strong consonance overwhelms dissonance from lattice tones. This makes the minor triad locally consonant. Octave transformations of these notes also retain this property. Thus, 20 and 24 have been added to the instrument. I ran out of space for 40 and 48.
2. Quiet sounds. Lattice tones scale faster than prime-ratio harmony and disappear at low volume. So while 1/6, 1/7, 1/8 is very dissonant, it is not dissonant if played quietly. For quiet sounds, pairwise ratios decide consonance.
3. Locally consonant sounds with large frequency gaps. If lattice tones do not overlap frequencies, they have low pushing strength. For example, 1 and 6/5 and 6 and 5 8 are consonant. These pairs are less consonant when put together, but their lattice tones barely interact, so the sequential harmony takes precedence. Note that if we doubled the pitch of the first phrase to 2 and 12/5, the amalgam would be very dissonant.
4. Small consonance gradients from lattice tones too far apart. For example, 1.1 10 12 is not locally consonant, because moving 1.1 to 1 makes it more consonant. However, 1.1 interacts weakly enough with the other frequencies that the sound is consonant overall, and a voice can stick to 1.1 instead of moving to 1.0.
5. Small consonance gradients from lattice tones of too-high order. If arithmetic sequences are far from small ratios, the pushing force is small. For example, 5 7 9 and 4.9 7 9.1 are similar in behavior, and so are 5 7 8 and 5.1 7 7.95. The linear combination that would align these is 5a - 7b, which is too weak to be heard. The piano can't play any of these variations either.
6. Maximized dissonance. The tritone explicitly avoids consonance. So do tone clusters.

Most sounds can be played. For example, in the Passepied demo, the chords that can't be played are a minor chord out of range (15 40 48), the tritone at an octave (>2.83< 8 9), and the tritone repeating a prior note (15 >21.6< 40 48). The minor chord is fixed with more keys, but the tritones are not. Debussy bridges the Romantic and Modern eras, so this demo is mildly explorative in dissonance.

Maximally dissonant chords can only be approximated. It's no surprise they cause trouble for a consonant instrument. Tritones can be played as either 7/5 = 1.4 ≈ 1.414, 10/7 = 1.429, or 45/32 = 1.406. As notes are added to a chord, these approximations may be blocked. The diminished seventh is especially dissonant, and there's no hope for rational approximation there. Tone clusters can be played as 14-15-16.

Since you got to the end, here's a secret button that puts the green numbers on the instrument in descending order. It breaks the green text links and playing randomly doesn't sound good anymore, but it might be easier to find numbers.